Reinforced siding is a structural form widely used in aircraft structures. In addition to the damage forms such as cracks, the reinforced panel fastening joints such as rivets and bolts can also be seen as a form of damage. The detection of such fastener loosening damage is one of the main tasks of aircraft structural health monitoring. Damage detection is the core and foundation of structural health monitoring technology [1]. At present, most vibration-based damage detection methods are carried out in the frequency domain. In practice, the direct test of the structure is the time-domain vibration response signal of the structure, and the signal is from the time domain. Transforming into the frequency domain not only brings computational errors, but also makes real-time detection of damage difficult. Using the time domain vibration response signal of the test to directly extract the damage characteristic parameters can not only avoid the error caused by the data time-frequency transform, but also has the advantages of online and real-time detection. In [2], the cross-correlation function magnitude vector (CorV) composed of the amplitude of the cross-correlation function of the vibration response between the various measuring points is used as the damage index, and the damage of the structure is detected by the change, and applied to the aircraft siding structure. The damage detection experiment of fastener loosening [3] has obtained good test results. On the basis of CorV, the literature [4] proposed an damage detection method based on inner product vector (IPV), and successfully detected the damage of composite beam model under different noise levels. However, CorV and IPV based damage detection methods need to define a reference point in the detection process. If the test accuracy of the response at the reference point is not high, it may affect the detection effect, that is, the above method implies a reference point response test. Strict requirements for reliability.
In this paper, a method for detecting structural damage by directly using the autocorrelation function of structural response without defining a reference point is developed, and the effectiveness of the method is verified by the test of the loosening damage of the aircraft stiffened panel fastener. Applicability in real-time detection.
1 Damage index based on autocorrelation function
1.1 Autocorrelation function of acceleration response
Assuming that the structure of the n-degree system is under white noise excitation and the excitation is at the k-point of the structure, the autocorrelation function of the structure i-point displacement response x ik (t) can be written as [5]:
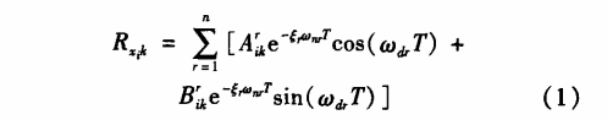
among them:
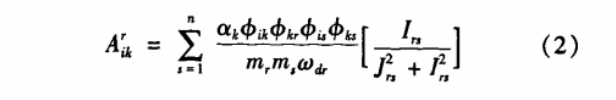
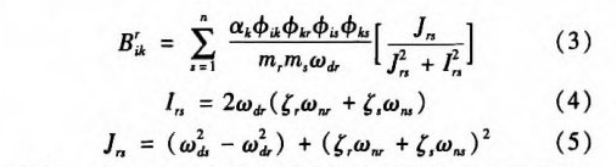
Where a k is a constant related to the statistical properties of the white noise excitation, ф ik represents the ith component of the rth mode, and m r , ζ r , ω nr , ω dr represent the rth modal quality, Damping ratio, undamped natural frequency, and damped natural frequency.
Since the response of the structure in the case of white noise is a stationary stochastic process, and for a (weak) stationary stochastic process, there are [6, 7]:
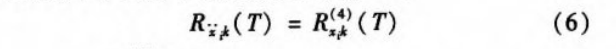
Is the fourth derivative of the delay T for the autocorrelation function R xik , 
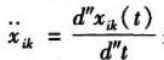For the acceleration response, the detailed proof process of equation (6) can be found in [8], acceleration response. 
The autocorrelation function is: 
From equation (7), the k-point excitation can be obtained, and the structure i-point response (hereinafter, unless otherwise specified, the "response" refers to the acceleration response) is the value of the autocorrelation function at time delay T=0.
: 
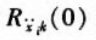In order to eliminate the influence of the magnitude of the incentive force,
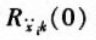Normalize to a maximum of 1: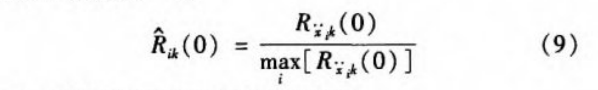 
1.2 Damage indicators based on autocorrelation function
Establish the following damage indicators:
among them,
, 
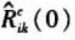The normalized i-point reference response and the characteristic response autocorrelation function zero point value. It can be seen from equations (8), (9), and (2) to (5) that the zero point value of the autocorrelation function normalized by each response point of the structure is obtained. 
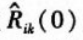Only related to the modal parameters of the structure, the damage index D i is only related to the structural modal parameters. When the structural health state changes, the structural modal parameters will also change, and the damage index D i will inevitably change, and the change can be used to detect the damage. 2 Damage detection of reinforced wall panel fasteners
2.1 Damage detection experiment
The reinforced siding structure used in the experiment is shown in Fig. 1. The web is 0.5 mm thick aluminum plate, and the fastener is mounted on the frame made of aluminum ribs. In order to simulate both the intact and loose fasteners, easy to handle bolts and fasteners are used to secure the ribs and webs. The wall panel is fixed to the test bench by a clamp cantilever, as shown in Fig. 1, the excitation point is located at the left end of the wall plate, and the excitation direction is perpendicular to the plane of the wall plate.
In the middle rib position of the siding, an accelerometer is placed every two bolts. The bolts and accelerometers are numbered as shown in Fig. 2. The numbers without brackets indicate the accelerometer number, and the numbers with brackets indicate the bolt number. The state in which all the bolts of the wall plate are fastened is regarded as the intact state of the structure, and the natural frequency in the intact state of the wall plate is measured by the sine sweep frequency method, and the sweep frequency range is set to 0 Hz to 100 Hz. The result of taking 10 sweep averages is taken as the natural frequency of the structure, and the first three natural frequencies measured in the intact state are 10.27 Hz, 53.15 Hz, and 67.26 Hz, respectively.
The LMS SCADAS III system generates a 0Hz~15Hz white noise excitation signal with a bandwidth of only the structural fundamental frequency to drive the exciter to excite the wall plate, and collect the response of each accelerometer in a structurally intact state; loose a bolt on the wall panel The open state is regarded as the damage state of the structure, and the local details of the loose damage are as shown in Fig. 3. Each bolt is loosened, the excitation bandwidth is kept constant, and the response of each accelerometer in the loose state of each bolt of the structure is collected.
2.2 Damage test results
Here, the damage detection results of three typical working conditions are given. The structural state of each working condition reference response and characteristic response is shown in Table 1. According to the definition of the damage index in Section 1.2, various working conditions can be calculated. The value of the lower damage index varies with the position of the measuring point, as shown in Fig. 4. The maximum value of the damage index for each working condition is given in Table 1.
It can be seen from Table 1 that the maximum value of the damage index of working condition 1 and working condition 3 is different from the maximum value of the damage index of working condition 2, that is, when the structural state has not changed, the maximum value of the damage index is relatively small. When the structural state changes, the maximum value of the damage index is relatively large. In addition, as can be seen from Fig. 4(b), when the structural state changes, the maximum value of the damage index is located at the measuring point 4, and the measuring point closest to the loose bolt 6 is the measuring point 4. That is, when it is determined that the structural state has changed (such as structural damage), the damage location is near the measurement point of the maximum value of the damage index. The test results after the bolts are loosened in other positions have the same rule.
This is because when the structural state has not changed, the dynamic characteristics of the structure will not change or there will be only a small change due to environmental interference. The normalized characteristic response of each measuring point and the reference response autocorrelation function zero The difference in value is very small, and the value of the damage index is relatively small and irregular at each measuring point, as shown in Fig. 4(a) and Fig. 4(c). When the structural state changes, the structural dynamics near the loose position of the bolt The change of the learning characteristics is particularly obvious. This shows that the normalized characteristic response and the reference response autocorrelation function zero value change greatly near the damage position, while the other positions change relatively small, which is the damage index. There is a maximum value near the damage location, and is much larger than the damage index values ​​of other locations, as shown in Figure 4(b).
3 Applicability analysis of real-time detection of loosening damage
Under the premise of selecting the excitation signal bandwidth, the white noise excitation generated by the LMS SCADAS III system is only the signal of the power spectrum approximation. That is, the damage detection experiment in this paper is actually performed under the white noise excitation of the power spectrum approximation. Therefore, the damage detection method in this paper does not require the excitation before and after the structural damage to be completely consistent, and only needs to achieve the same power spectrum, which is of great significance for the real-time detection of structural damage.
It can be seen from the detection rule obtained in Section 2.2 of this paper that when the structural state is unchanged, the damage index value changes little; and when the structural state changes, the damage index value of the measuring point near the damage position will increase significantly ( The change in magnitude), so the damage index value of each measuring point at each moment can be monitored to monitor the looseness of the fastener in real time.
3.1 Real-time detection experiment
The application of the real-time test results of the loosening of the stiffened panel fasteners is used to illustrate the applicability of the method in the real-time detection of such structural fasteners. Under the excitation of 0Hz~15Hz white noise, firstly, a response of each measuring point in the structurally intact state is used as a reference response to calculate the zero point value of the autocorrelation function, which is normalized.
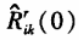Value; under the premise of the unknown structural health state, the response of each measuring point is collected at regular intervals, and each segment of the collected response is divided into 16 segments, and the zero value of the autocorrelation function is calculated separately, which is normalized. 
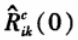The value, in turn, the damage index Di for each measurement point. 3.2 Real-time detection of experimental results
Figure 5 shows the change of the damage index value of each measuring point before and after the bolt 7 is loosened with the acquisition time period. It can be seen from Fig. 5 that the damage index value of the measuring point 4 has increased to a very large position compared with the other measuring point damage index values ​​in the period 4 and the period 5, and remains substantially unchanged, while the damage index of other measuring points The value is basically unchanged. It can be determined from the law in Section 3 that the loosening of the bolt occurs between the period 3 and the period 4 in the vicinity of the measuring point 4. The actual simulated damage is the loosening of the bolt 7 near the measuring point 4 after the time period 3, that is, the result of the real-time testing experiment is consistent with the actual simulated damage time and the damage position. Real-time detection of bolt loosening at other locations has the same result, so the damage detection method proposed in this paper is suitable for real-time detection of such damage.
4 Conclusion
In this paper, the damage index is constructed by using the zero point value of the autocorrelation function of the acceleration response of each measuring point under the excitation of white noise. The experiment of loosening damage detection and real-time detection of the fasteners in the stiffened wall structure shows that:
(1) With the method of this paper, only the excitation bandwidth needs to be selected, and the excitation bandwidth only includes the fundamental frequency of the structure to ensure accurate positioning damage.
(2) The damage index proposed in this paper is only related to the modal parameters of the structure, but it can accurately locate the fasteners of the slab structure by using the acceleration response of each measuring point without modal parameter identification. s position;
(3) The method in this paper is applicable to the real-time detection of damage such as the looseness of the wall structural fasteners.
(4) Similar to many existing vibration-based damage detection methods, one limitation of the method is that more points are needed. How to optimize the position and quantity of the measurement points is a future research direction.
references
[ 1 ] Sohn HS, Farrar CR, Hemez FM, A review of structural health monitoring literature: 1996-2001 [R]. Los Alamos National Laboratory Report, LA 13976 MS, 2003.
[ 2 ] Yang ZC, Yu ZF, Sun H, On the cross correlation function amplitu devector and its application to structural damage detection [J]. Mechanical Systems and Signal Processing, 2007, 21:2918-2932.
[3] Yang Zhichun, Yu Zhefeng. Experimental study on loosening damage detection of aircraft siding fasteners based on cross-correlation function amplitude vector [J]. Aircraft Engineering, 2006, 1:62-66.
[4] Yang ZC, Wang L, Wang H, et al. Damage detection in composite structures using vibration response under stochastic excitation [J]. Journal of Sound and Vibration, 2009,325: 755-768.
[ 5 ] James GH III, Carne TG, Lauffer JP. THE Natural Excitation Technique (NEXT) formodal parameter extraction from operating structures [J]. Modal Analysis: The international Journal of Analytical and Experimental Modal Analysis, 1995, 10(4): 260-277.
[6] Bendat JS, Piersol AG. Random Data: Analysis and measurement procedures, 3rd Edition [M]. Willey, New York, 2000.
[7] Papoulis A, Pillai SU. Probabillity, random variables and stochastic processes, 4 the dition[M]. Mc Graw Hill, New York, 2002.
[ 8 ] Wang Le. Theoretical and experimental research on structural boundary condition parameter identification and structural damage detection [D]. Xi'an: Northwestern Polytechnical University, 2010, 3.
AAG Furniture Hinges are designed to provide an effective solution to hanging doors and cabinets,where there is a need for high grade quality hinges. They are made from high grade steel or SS304 material and are suitable for both interior and exterior doors and cabinets where a hinge is required or when being used in conjunction with a door or a cabinet use, we appreciate the simplicity of a quality hinge as well as the value this essential hardware can bring to one`s everyday life.
Please send us enquiry for these furniture hinges.
Door Hinge,Iron Door Hinges,Cabinet Hinge,Bearing Door Hinges
Foshan Nanhai Xin Jianwei Hardware Co., Ltd , https://www.aaghardware.com